Instead, consider that the 2.07% probability is implying that the outcome is about 33% (0.51/1.56 = 0.33) more likely than it actually is.Ī single bet, for comparison, implies the outcome is just 4.8% (2.38/50 = 0.048) more likely than it actually is.Īnd obviously, you’re much more likely to find edges attacking a 4.8% gap than a 33% one. You take the Kings line which is positive +140 so.
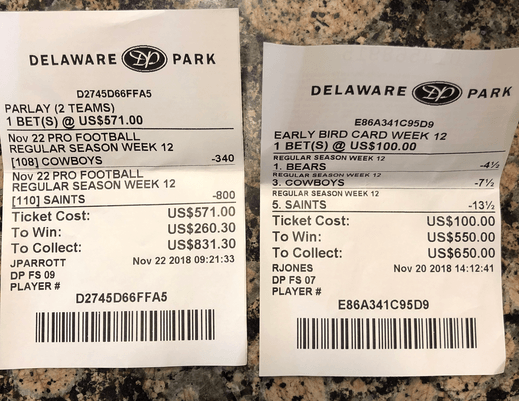
That’s not, however, how the comparison should be read. You want to Parlay the Los Angeles Kings at +140 and the Calgary Flames at -135 for a 100. I mean, the odds of hitting a five-team parlay are only 0.51 percentage points less than what the books are implying … that sounds like nothing. The following table illustrates how the chances of winning parlays compares to the payouts received as the number of bets is increased (assume each bet comes at the standard -110 juice and has a 50% chance of winning).Ĭomparing the percentages may not do justice to the difference between the implied and true probabilities at first glance. While the payouts are certainly appealing, they’re not as high as they should be given the true chances of a given parlay winning. Mathematically speaking, it’s usually not a good idea to bet parlays. In sports, a parlay bet is a wager you can place on multiple outcomes on the same betting slip.